Implementing your Own 2D game engine

First of all, you would think that when there are so many game engines out there why would you want to implement your own. Well it may be that you don't like any of them, or just thinking of starting a game and implementing your own engine might be a good idea, then please don't do it and this article might not be for you. But if you (like me), want to learn nitty-gritty of a physics engine, this could be a good exercise.

Here is the demo of the end result and you can find the code on my github.

In this article I won't be providing any code snippets since you can find that in the github link I have provided above, but more of an explanation of how things are pieced together.

First, we will start with some basic assumptions:

All bodies are rigid bodies means they cannot deform on impact.
Colliding shapes of rigidbodies are convex, non-convex shapes should be bounded by a convex shape for collision detection purposes.
Physics simulation runs at a constant frame rate i.e usually 60 fps.
Whatever I will be describing has been implemented for 2D but most of the general idea is applicable for 3D as well. Also, the processes I have described is what I have implemented, different game engines tend to use different models or optimizations.

Overview

For a physics engine to function properly it should perform three basic things:

It should be able to predict translational properties like position, velocity, acceleration and rotational properties like orientation, angular velocity, torque at any given point of time.
It should be able to detect which bodies are colliding.
It should be able to properly resolve the impulses generated due to those collisions.

Calculating Properties

For calculating the properties we basically use Newton's Law of motion. $v = \int 1/ m * F d t$ and, $x = \int v d t$ where,

F = force applied
v = Velocity
m = mass of body
x = position
dt = time elapsed since last execution (1\60 if 60 fps)

To solve these differential equations for games, we widely come across these three integrator:

Explicit Euler method

It is the most basic method to solve this first order differential equation. It is just adding the curve values at small intervals. $x_{n + 1} = x_{n} + v (t_{n}) * d t v_{n + 1} = v_{n} + a (t_{n}) * d t$
Implicit (Symplectic) Euler

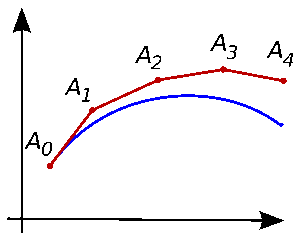
The difference here is we solve the problem using right Reimann sum rule instead of left sum rule. For those who are not going to read wikipedia, reimann sum is used to calculate the area of the region by breaking it into small shapes. In euler methods region is a rectangle.

For example to get position at time t, we will need velocity at time t+1, so instead of starting with zero velocity we compute velocity first and then position. $v_{n + 1} = v_{n} + a (t_{n + 1}) * d t x_{n + 1} = x_{n} + v (t_{n + 1}) * d t$
Runge-Kutta (RK) 4th Order Method

I won't be going into much explanation about what it does, but it gives better accuracy than euler methods but is computationally expensive. Actually, Euler methods are just a special case of RK.

Implicit euler gives us more accurate results than explicit euler and is much closer to RK4. Here is a more detailed comparison of all three methods and is explained why implicit euler is okay for game engines.

So using implicit euler we will get:

 v += (1/m * F) * dt   # velocity
 x += v * dt           # position

If we take rotation into account,

ω += (1/I * τ) * dt
θ += ω * dt

where,
I = Moment of Inertia
θ = orientation
ω = angular velocity
τ = Torque

Calculate colliding pairs of rigidbodies

At each loop it is necessary for engine to know which pair of rigidbodies are colliding, so that the collision can be solved and bodies do not pass each other.

Naively if we iterate on all N bodies, we will need to check N*(N-1)/2 possible combinations which are a lot. Suppose N = 100, we will need to check 4950 body pairs which can take way too much than the frame duration (i.e just 1/60s or 16ms). In most of the games there are more objects present than that at any given point of time.

So first we use a process called BroadPhase calculation to narrow down the number of collisions to check. Its purpose is to generate a list of pair of rigid bodies that may be colliding.

It is implemented through Space Partitioning algorithms.
The basic idea is that you divide the whole region into grids (in volumes for 3D) and assign every body to a position in the grid.
Now, the body is added to each cell it is overlapping, so at last we iterate through grid and make pair of overlapping bodies. Objects are stored in data structures like k-d tree or BSP tree for efficiency. It generally reduces the iterate time from O(N²) to logarithmic times. You can find more in depth details of the broadphase implementation, like choice of grid size, etc. My demo was just for a small scope, so I have not implemented this part.

Then we proceed to NarrowPhase calculation i.e which actually determines which bodies are colliding. Aim of Narrowphase is to calculate three things for every pair of colliding bodies:

Collision Normal: Direction of bodies they are colliding
Penetration Depth: How much bodies have overlapped each other
Contact Points: Points of contact where they are overlapping

It can be implemented using Separating Axis Theorem. The basic principle is: If two bodies are not colliding, there will be a certain axis for which their projections will not overlap.

For a general convex polygon there could be a lot of axes to check, but for simplification purposes, I have just taken the shape of the colliders to be Circle and Axis-Aligned Bounding Box (AABB) i.e just a rectangle. Now for collision checks, we will like to implement four combinations (not taking rotation into account):

Circle-Circle

For this, test is easy - Distance between circles should be less than sum of their radii

// distance must be less for overlap
isColliding = distance(circle1, circle2) <= circle1.radius + circle2.radius

Circle-AABB / AABB-Circle

We will first find the nearest point of contact on AABB between AABB and circle.

positionDiff = AABB.pos - circle.pos

// on x-axis take the point which is near, the bounds or diff
nearestPoint.x = clamp(-AABB.width/2, AABB.width/2, positionDiff.x)
// same for y-axis
nearestPoint.y = clamp(-AABB.height/2, AABB.height/2, positionDiff.y)

// distance between nearest point on rectangle and circle's center should be less than circle's radius
isColliding = distance(circle1, nearestPoint) <= circle.radius

AABB-AABB

positionDiff = AABB2.pos - AABB1.pos

// find overlap values
xOverlap = AABB1.width/2 + AABB2.width/2 - abs(positionDiff.x) // x-axis overlap
yOverlap = AABB1.height/2 + AABB2.height/2 - abs(positionDiff.y) // y-axis overlap

// for bodies to be colliding both axis must overlap
isColliding = xOverlap > 0 && yOverlap > 0

For a convex polygon its implementation will be more complex, there is a good video in GDC Vault explaining the process. Also you can go through the Box2D code for the same. It is next in my list for implementation.

Impulse Resolution

Impulse resolution means when bodies collide, we need to stop them from moving inside each other. The first thing that comes to mind is that we can apply a force to them, but force does not instantaneously change the velocity. For this we directly change the velocity of the bodies or say we applied an impulse (i.e you can think of it as a large force in almost zero time).

Each rigidbody apart from dynamic properties also has some physical properties which we group into Material.

Mass (m): how much the body weigh
Coefficient of restitution (e): how rough is the surface
Coefficient of Static friction (μ_s): friction coefficient for stationary objects
Coefficient of dynamic friction (μ_d): friction coefficient for moving objects

For a pair of bodies we calculate equivalent coefficients.

Equivalent coefficient of restitution is e = min(e1, e2).
Equivalent coefficients of friction are: $μ_{s} = μ_{s 1} * μ_{s 1} + μ_{s 2} * μ_{s 1} μ_{d} = μ_{d 1} * μ_{d 1} + μ_{d 2} * μ_{d 1}$

During the time of contact we will consider two impulses acting on them:

Normal Force (Normal to the plane of contact)
Frictional Force (Tangential to the plane of contact)

Impulse (j) is calculated using Momentum Conservation and Newton's law of restitution.

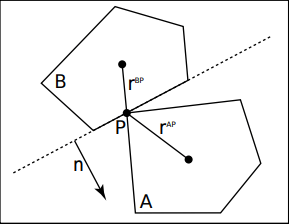
Normal Impulse

Let us define some variables,

v_A, u_A = final and initial velocity of body A
v_B, u_B = final and initial velocity of body B
j_A = change in momentum of A
j_B = change in momentum of B
n = normal vector in direction of collision normal (n.n = 1)

According to Newton's law of restitution,

e = relative final velocity / relative initial velocity

Since momentum is conserved change in momentum of Body A will be opposite to the change in momentum of body B i.e j_A . n = -j_B . n. Taking a dot product with n since we are interested only in normal direction.

$e = \frac{- ( v _{B} - v _{A} )}{u _{B} - u _{A}} j_{A} . n = m_{A} (v_{A} - u_{A}) j_{B} . n = - j_{A} . n = m_{B} (v_{B} - u_{B}) u_{A B} = u_{A} - u_{B}$

So our aim is to calculate j in terms of initial velocity since we don't know the final velocities of bodies after collision. We will just rearrange the terms:

$v_{A} = u_{A} + \frac{j _{A} n}{m _{A}} v_{B} = u_{B} - \frac{j _{A} n}{m _{B}} v_{B} - v_{A} = e u_{A B} = - u_{A B} - j_{A} n (\frac{1}{m _{A}} + \frac{1}{m _{B}}) j_{A} = - j_{B} = - \frac{( 1 + e ) u _{A B} . n}{( \frac{1}{m _{A}} + \frac{1}{m _{B}} )}$

Whew, that's a lot of equations, but don't worry that's just rearranging the terms to get what we need, you can work it out yourself.

If you want to rotational motion into account, its easy, like linear momentum, angular momentum is also conserved. Let us define more terms so that further equation can be clear.

L = angular momentum
p = linear momentum
I = Moment of Inertial about Center of Mass (COM)
r = radius vector perpendicular to COM

Some basic definitions, $L = I ω = r x p v_{A}^{t o t a l} = v_{A}^{l in e a r} + r_{A} ω_{A} Δ L = I \frac{Δ v _{an gu l a r}}{r}$ When considering the change in linear momentum also add angular momentum giving us final equation: $j_{A} = - j_{B} = - \frac{( 1 + e ) u _{A B} . n}{( \frac{1}{m _{A}} + \frac{1}{m _{B}} ) + \frac{( r _{A} . n ) ^{2}}{I _{A}} + \frac{( r _{B} . n ) ^{2}}{I _{B}}}$

Frictional Impulse

Frictional Impulse is applied perpendicular to collision normal.

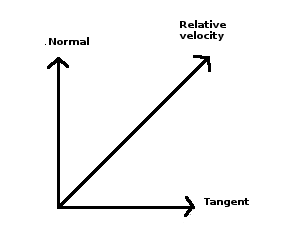
Frictional impulse can be calculated by just substituting normal vector with the tangential magnitude of relative velocity and in opposite direction.

Replace n with t: $j_{f} = - \frac{( 1 + e ) u _{A B} . t}{( \frac{1}{m _{A}} + \frac{1}{m _{B}} ) + \frac{( r _{A} . n ) ^{2}}{I _{A}} + \frac{( r _{B} . n ) ^{2}}{I _{B}}}$ Now we just need to calculate t. For that we will get normal component of relative velocity and subtract from total relative velocity to get tangential component (Vector Math). Negative sign is used since friction is always opposite to the direction of motion. $t = - [V_{A B} - (V_{A B} \cdot n) * n]$

But wait there is a catch, friction acts differently for static and dynamic objects, that is why two coefficients of friction. How to use them can be determined using Coulomb's Law.

j_f <= μj_n

Let us understand this definition, if our solved jf (representing the force of friction ) is less than μ_static times the normal force (jn), then we can use our jf magnitude as friction. If not, then we must use our normal force times μ_dynamic instead.

if (abs(jf) < μ_sjn) {
    // no change
} else {
    jf = μ_djn
}

Hopefully you can now begin to understand the basics of writing a game engine, and again you can find the code on github. I have tried to include most of the topics that are absolutely required to implement a working demo. Now you can read up articles for specific topics to understand them more and how it will benefit your implementation.