Natural Looking Trees with Stochastic L-Systems

No Man's Sky is built around a procedurally generated deterministic open world universe with too many planets to be explored realistically. It is claimed that they used Superformula and L-Systems for generating flora and fauna procedurally. So, I tried playing around with L systems and see if I can create some realistic looking trees.

What is a L-System

An L-system or Lindenmayer system is a recursive and string-rewriting framework that was discovered by Hungarian biologist Aristid Lindenmayer while studying algae growth. Nowadays, in computer graphics it is used for creating procedural and fractal like structures. I won't go into much depth about it, since it is described quite elaborately on wikipedia.

There are mainly three types of L systems:

1. Deterministic Grammar
   • Context Free
   • Context Sensitive
2. Stochastic Grammar
3. Parametric Grammar [Not covered in this blog]

Above, I have created a small interactive demo which can generate different types of L systems and you can see how it grows over generations. You can select different examples from the dropdown. To learn more about how it is rendered see rendering section.

Deterministic Grammar

In deterministic grammar the system always generate a fixed output because the predecessor is always fixed. It can be further divided into two subtypes:

Context Free

In context free grammar, each token is evaluated in the isolation. For example:

$$\begin{array}{rl}Axiom& :X\\ Constant& :X\\ Rules& :\\ F& \to FF\\ X& \to F-[[X]+X]+F[+FX]-X\end{array}$$

Here when started with the axiom X,¹ both replacements will happen independently for single tokens i.e F and X.

Context Sensitive

Contrary to context free systems, in context sensitive rules can be defined for symbols to match when it is proceeded or succeeded by specific symbols. It can be used along with context free rules to propagate a symbol in certain direction for simulating signal propagation. These context rules are defined using < and > in the rule, near the predecessor or successor.

For example rule B < A -> B means that change A to B only if there is a B before A. Similarly you can have rules with either side.

$$\begin{array}{rl}A>B& \to B\\ B<A>B& \to C\end{array}$$

First one means change A to B only if there is a B after A. Second one means change A to C only if there is a B before and after A. Consider the following system:

$$\begin{array}{rl}Axiom& :BAAAAA\\ Rules& :\\ & B<A\to B\\ & B\to A\end{array}$$

Now if you apply these rules on the axiom it will result in simulating B moving right.

Pass0 => BAAAAA
Pass1 => ABAAAA
Pass2 => AABAAA
Pass3 => AAABAA
Pass4 => AAAABA
Pass5 => AAAAAB

In the above example, sometimes people get confused that if first B turns into to A then how does second A turns to B. It is because you have two generations of axiom, you don't change the second letter based on new value of first letter but old value of first letter. For example in Pass0 -> Pass1 if I go letter by letter and apply rules:

// pass0 -> pass1
     B   ->   A  // rule 2
     A   ->   B  // rule 1 because before A there is a B
     A   ->   A  // no rule match hence same
     A   ->   A  // no rule match hence same
     A   ->   A  // no rule match hence same
     A   ->   A  // no rule match hence same

Stochastic Grammar

You cannot generate infinite variations of even same type of tree with these fixed grammar. So, for creating an infinite world we need to introduce some sort of randomness for generating the next iteration.

It is simple to put randomness in generating this code structure. A simple example is given below.

$$\begin{array}{rl}Axiom& :F\\ Rules& :\\ p_1& :F\stackrel{0.33}{\to }F[+F]F[-F]F\\ p_2& :F\stackrel{0.33}{\to }F[+F]F\\ p_3& :F\stackrel{0.34}{\to }F[-F]F\end{array}$$

The idea is when replacing a token choose the replacement based on certain probability [here 1/3]. Thus it will generate different variant of same species of plant.

You can also play around with above interactive demo to generate more variations.

Rendering

There are a lot of methods for visualizing a L-system, but the easiest and mostly widely used is Turtle Graphics. I am pretty sure most of you have played around with turtle graphics in the past on MSLogo.

First we need to define Turtle and its state. A state of the turtle is defined as a triplet (x, y, α), where the Cartesian coordinates (x, y) represent the turtle’s position, and the angle α, is interpreted as the direction in which the turtle is facing. For every token we calculate the new state of turtle and apply the changes.

Token	Meaning
[A..Z]	Any non constant which tells turtle to move forward a fixed length, like FD 40
+	Moves turtle a fixed degree to right
-	Moves turtle a fixed degree to left
[	Push the current turtle state on stack
]	Apply the stack's last pushed state to turtle

Constants are tokens which are ignored during rendering.

class Turtle {
  constructor(fixedAngle, fixedLength) {
    this.fixedAngle = fixedAngle;
    this.fixedLength = fixedLength;
    this.position = new Vector2(0, 0); // x, y
    this.angle = 0; // α
    this.stack = [];
  }
}

Let us consider the example:

Code: F[+F]-F
FixedLength: 10
FixedAngle: 45°

Let us render the code token by token:

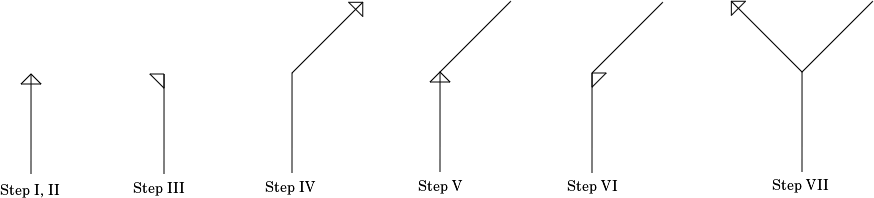
Steps	Token	Action
Step I	F	It will just move turtle by fixed length i.e 10 units in forward direction
Step II	[	This will just save the current state, i.e (0, 10, 90 deg) in the stack
Step III	+	It will just move the turtle right by 45 degrees
Step IV	F	It will move the turtle by fixed length in forward direction
Step V	]	It will apply the last saved state i.e what we saved in Step II
Step VI	-	It will just move the turtle left by 45 degrees
Step VII	F	Again move the turtle forward by length 10 units in forward direction

You can also refer the below for rendering.

class Turtle {
  ...

  // @param ctx: Js Canvas context
  // @param token: current token that is to be evaluated
  // @param constants: list of tokens that is to be ignored for rendering
  draw(ctx, token, constants) {
    if (constants.contains(token)) {
      return
    }

    this.validTokenRegex = new RegExp("[A-Z]")

    if (this.validTokenRegex.test(token)) {
      let newX = this.position.x + this.fixedLength * Math.cos(this.angle);
      let newY = this.position.y + this.fixedLength * Math.sin(this.angle);

      ctx.lineTo(newX, newY); // draw the line to new position
      ctx.moveTo(newX, newY); // move the turtle to that position
      this.position.set(newX, newY);

    } else if (token == '+') {
      this.angle -= this.fixedAngle;
    } else if (token == '-') {
      this.angle += this.fixedAngle;
    } else if (token == '[') {
      this.stack.push({ "positionX": this.position.x, "positionY": this.position.y, "angle": this.angle });
    } else if (token == ']') {
      let val = this.stack.pop();
      this.position.set(val.positionX, val.positionY);
      this.angle = val.angle;
    }
  }
}

Footnotes

References

1. The Algorithmic Beauty of Plants
2. Job Talle - Lindenmayer Systems