Generating Convex Hull using Graham Scan

I am trying to experiment with rendering some basic shapes on a pixel buffer for another side project of mine. After trying out a few rust crates out there and not liking any, I eventually fell into the classic software engineering trap and wrote a small library - ada. It supports some basic shapes like - Line2D, Rectangle2D, Ellipse2D, Polygon2D and Bezier2D.

For polygons I wanted to create random shaped convex polygon. One way to do that is to generate a set of random points and compute its convex hull. There are many convex hull algorithms but the one we are discussing below is Graham Scan which takes O(n log n) time.

Visualizing Steps

Here is a demo of the steps the algorithm takes.

How does it work

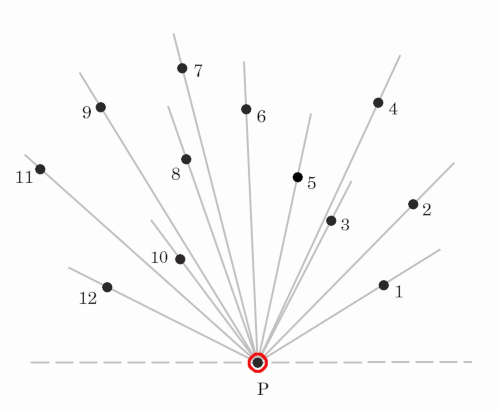
Step1: Get the bottom most point P

We will start by finding the point with lowest y coordinate. If two points have same y-coordinate we will take the one with least x-coordinate. In the above demo, bottom most point is colored red.

Here is the code to find bottom-most point:

class GrahamScan {
  constructor(points: []Vector2) {
    this.points = points;
    this.startPointIndex = undefined;
    this.stack = [];
  }

  function getBottomMostPoint() {
    var bottomIndex = 0;
    for (let i = 1; i < this.points.length; i++) {
      let pTry = this.points[i];
      if (pTry.y < this.points[bottomIndex].y ||
            (pTry.y == this.points[bottomIndex].y && pTry.x < this.points[bottomIndex].x)) {
        bottomIndex = i;
      }
    }
    this.startPointIndex = bottomIndex;
  }
}

We only iterate through the array once, hence time complexity till now is O(n).

Step2: Sort the points in increasing order of angle with x-axis

Next we will sort the points in increasing order of angle they and Point P make with x-axis. In the above demo, the result of this sorting is shown by drawing a blue line to each point from bottom-most point P. You can intuitively see that marked line moves in anti-clockwise direction.

For making a comparison of angles for sorting function, we can calculate cos θ using dot product, but that would be little inefficient and we can do better than that.

$cos θ = \frac{a . b}{∣ a ∣ * ∣ b ∣}$

We don't need to actually calculate the angle to sort. We can compare the angle made by any two points [Let's call them A and B] using just the cross product of $P A$ and $PB$ .

Calculate the cross product for ordered triplet [P, A, B], If

 $P A \times PB > 0$  => anti-clockwise means keep order as it is i.e A then B

 $P A \times PB < 0$  => clockwise hence swap the order i.e B then A

 $P A \times PB = 0$  => points are colinear, keep the one with least distance first

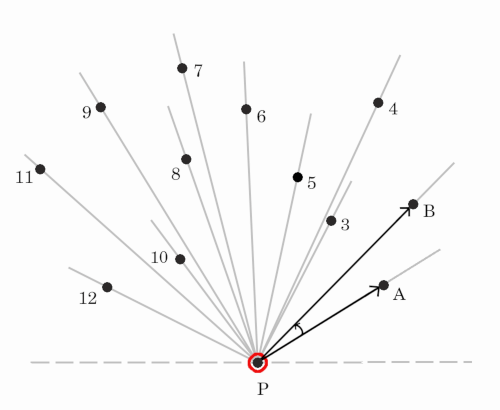
In the above picture if we get the order [P, A, B] then cross product will be positive keeping A first then B. Else if we get the order [P, B, A] then product will be negative, causing order to swap, again choosing A first then B.

Here is the code to implement sorting:

class GrahamSort {
  ...

  /**
   * To find orientation of ordered triplet (p, q, r).
   *
   * @param {Vector2} p, q, r
   * @return {number} wether points are clockwise, counter-clockwise or colinear
   *
   *  0 => colinear, 1 => clockwise and 2 => counter-clockwise
   */
  function orientation(p, q, r) {
    let val = (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);

    if (val == 0) return 0;  // colinear
    return (val > 0) ? 1 : 2; // clock or counter-clock wise
  }

  function sort() {
    // first remove the bottom most point in the array
    let startPoint = this.points.splice(this.startPointIndex, 1);

    // now sort rest of the points
    this.sortedPoints = this.points.sort((a, b) => {
      let o = orientation(startPoint, this.points[a], this.points[b]);
      if (o == 0) {
        return (distSq(startPoint, points[a]) >= distSq(startPoint, points[b])) ? -1 : 1;
      }
      return (o == 2) ? -1 : 1;
    });

    this.stack.push(startPoint);
  }
}

Sorting can be done via any of the O(n log n) algorithms like quicksort.

Step3: Scan the points for left turns

Let us create a stack to keep the points which will make the hull. First we push bottom most Point P and the next two points from sorted points into the stack.

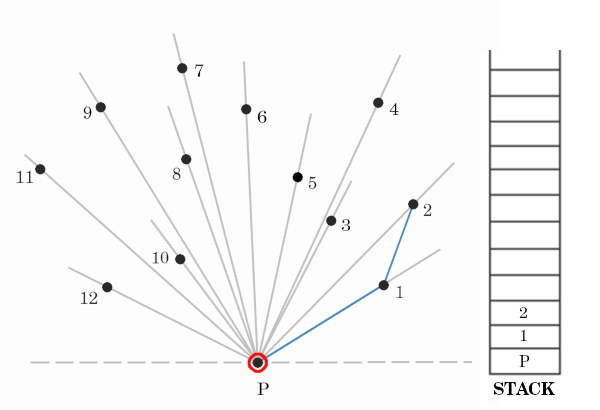
Now we will iterate through rest of the points and check wether we will add it in the stack or not. The check is as follows:

Calculate the orientation of ordered pair of last two points in stack and current point in consideration.
If orientation is:
- Anticlockwise i.e we took a left turn reaching this point, we consider it part of hull and add it in stack
- Collinear discard the current point
- Clockwise i.e we took a right turn to reach this point, we will temporarily keep this point. But we will keep removing previous points unless new point makes a left turn with last two points.
The points on stack will form a convex hull.

Consider the above image, On checking point 3, we see that we took a left turn to reach it with respect to last two points i.e 1 and 2. Hence we will add three 3 in the stack and consider it as part of hull for now.

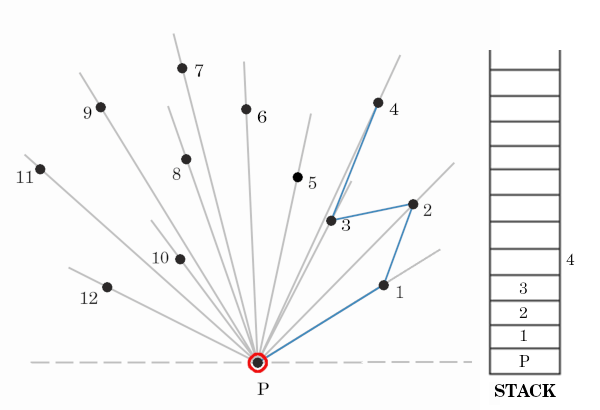
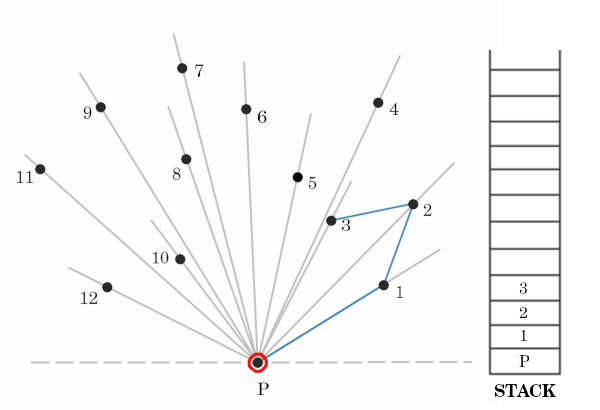
For the next point 4, we see that we have to take a right turn to reach it. Hence we will temporarily keep point 4 and pop previous point i.e 3 and check if point 2 and 4 make a left turn. If yes we will take out 3 and consider 4 as part of hull [as seen in below image].

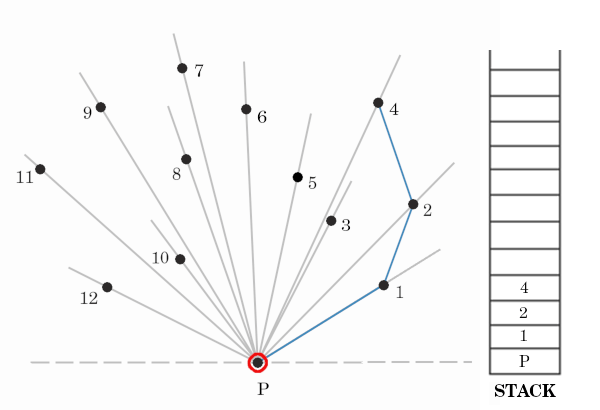
Well here is the code for final step:


class GrahamScan {
  ...

  function scan() {
    // push first and second point
    this.stack.push(this.sortedPoints[0]);
    this.stack.push(this.sortedPoints[1]);

    for (let i = 2; i < this.sortedPoints.length; i++) {
      // Keep removing top while the angle formed by points
      // next-to-top, top, and sortedPoints[i] makes a non-left turn
      let stackLength = this.stack.length;
      while (this.orientation(this.stack[stackLength - 2], this.stack[stackLength - 1], this.sortedPoints[i]) != 2) {
        this.stack.pop();
      }
      this.stack.push(this.sortedPoints[i]);
    }
  }
}

Well it might look like complexity for this step is O(n^2) because for adding each new point we might iterate back the whole loop. But when encountering the right turn, previous point is removed and doesn't get considered for iterating back for a future point. It means each point would only be considered at-most twice. So complexity of this step would actually be O(n).

Hence the final complexity of this algorithm will be O(n log n) with sorting taking the most time.

That's all folks, hope this makes sense.

References

Wikipedia