Uniform Random Distribution using Poisson Disc Sampling

Suppose you want to fill a texture or a 3D world with a object placed randomly like procedurally filling a forest with trees, random 2D distribution does not give good results.

Random Sampling vs Poisson Disc Sampling

Poisson Disc Sampling has many applications in games:

• uniform random object placement
• sampling for graphics applications
• procedural texture algorithms
• mesh algorithms

The one i would be focusing on is object placement.

Implementation

There are many implementations for poisson disc sampling but the one we are going to discuss was proposed by Robert Bridson¹. It is reasonably fast and can be used for N arbitrary dimensions.

The steps are as follows:

1. First we will define the minimum distance r that we want our points to have. Then a 2D grid is created with a cell-size $r/\sqrt{2}$ [See the below diagram for why].

Calculating Cell Size a

Let us then start with declaring some variables:

let radius = 10;
let cellSize = radius / Math.sqrt(2);

// number of columns and rows grid will have
let numColumns = Math.floor(canvas.width / cellSize);
let numRows = Math.floor(canvas.height / cellSize);

// initialize grid
let grid = new Array(numColumns * numRows);
grid.fill(undefined);

2. Next choose a random starting point in the 2D space. We will also define a variable activeList which will contain points which we still need to process. Put the startPoint in the grid as well as in activeList.

In my simulation starting point is either canvas center or the mouse click position. Points in pink color are the ones present in activeList.

// ...

let activeList = [];

function main() {
  var startPoint = new Vector2(canvas.width / 2, canvas.height / 2);
  var [si, sj] = toGrid(startPoint);

  // put the start point in grid and active list
  grid[sj + si * numColumns] = startPoint;
  activeList.push(startPoint);
}

function toGrid(v) {
  return [Math.floor(v.y / cellSize), Math.floor(v.x / cellSize)];
}

3. Repeat the below steps until activeList is not empty:

• Choose a random point from the activeList
• Generate k points [max tries in my simulation] randomly from an annulus [min distance r and max distance 2r].

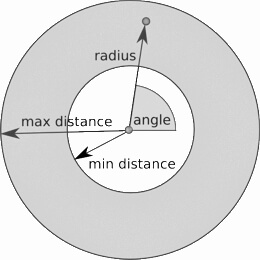
• For each generated point check if point already exists in grid at that position or if it is too close [< r] to any point. You need not check the whole grid, just checking the neighboring cells would work.
• If there is none, add this point to activeList and grid.
• If no new point is found, remove the current point from the activeList.

// ...
let maxTryLimit = 10;

function main() {
  var startPoint = new Vector2(canvas.width / 2, canvas.height / 2);
  var [si, sj] = toGrid(startPoint);

  // put the start point in grid and active list
  grid[sj + si * numColumns] = startPoint;
  activeList.push(startPoint);

  while (activeList.length > 0) {
    let index = MathUtil.randomInt(0, activeList.length);
    let activePoint = activeList[index];

    let sample = generateSample();
    if (sample) {
      grid[sampleGridIndex] = sample;
			activeList.push(sample);
    } else {
      // remove point from active list
      activeList.splice(index, 1);
    }
  }
}

function generateSample() {
  for (let n = 0; n < maxTryLimit; n++) {
		// generate a random 2d point between r and 2r radius from active point
    let randomAngle = MathUtil.randomFloat(0, 2 * Math.PI);
		let randomDistance = MathUtil.randomInt(radius, 2 * radius);
		let sample = new Vector2(
      activePoint.x + randomDistance * Math.cos(randomAngle),
      activePoint.y + randomDistance * Math.sin(randomAngle)
    );

		let [sampleGridI, sampleGridJ] = toGrid(sample);
		let sampleGridIndex = sampleGridJ + sampleGridI * numColumns;

		// before proceeding check if sample lies inside our boundary and no sample already
		// exists in the grid in that position
		if (sampleGridI < 0 || sampleGridJ < 0 || sampleGridI > numRows || sampleGridJ > numColumns || grid[sampleGridIndex]) {
			continue;
		}

    // check if point is atleast r distance away from 8 neighboring points
		if (isNeighborOk(sampleGridI, sampleGridJ, sample)) {
			return sample;
		}
	}
}

function isNeighborOk(grid_i, grid_j, sample) {
  for (let i = -1; i <= 1; i++) {
    for (let j = -1; j <= 1; j++) {
      let checkingIndex = (grid_j + j) + (grid_i + i) * numColumns;
      if (grid[checkingIndex]) {
        let distanceSqr = Vector2.distanceSqr(sample, grid[checkingIndex]);
        if (distanceSqr < radiusSqr) {
          return false;
        }
      }
    }
  }
  return true;
}

Effect of Max tries

Having a greater value of k [typically more than 30] will give you a dense packing while having a less value [< 5] can leave holes in the generation.

Though it can be desirable if you would want to fill those areas with some other things. For example with lakes when generating a forest. You can try playing around with MaxTries slider above to see the effect of k.

References

If you enjoyed the article and want to see more of these interactive tutorials then you can subscribe below.